2022 Testing stationarity of the detrended price return in stock markets
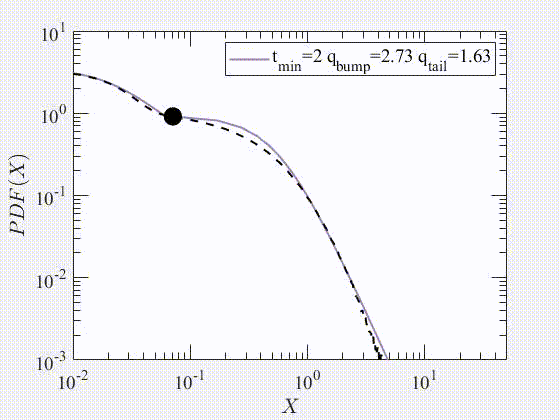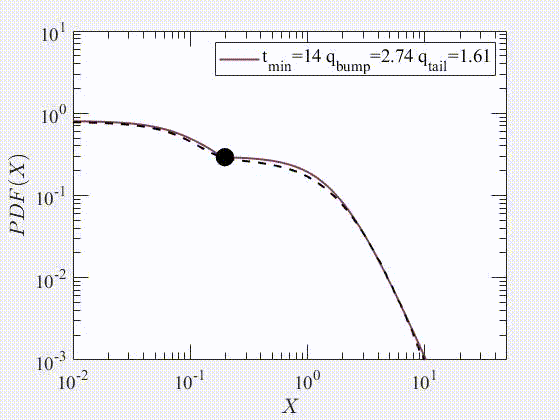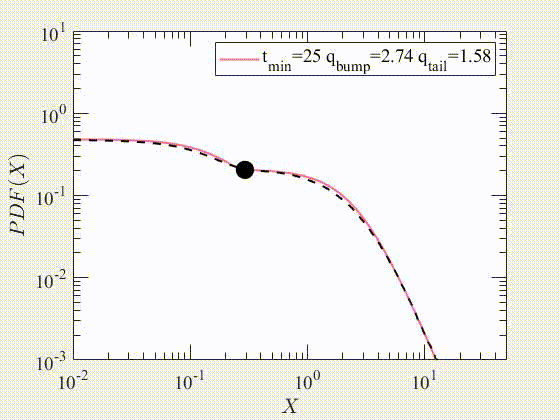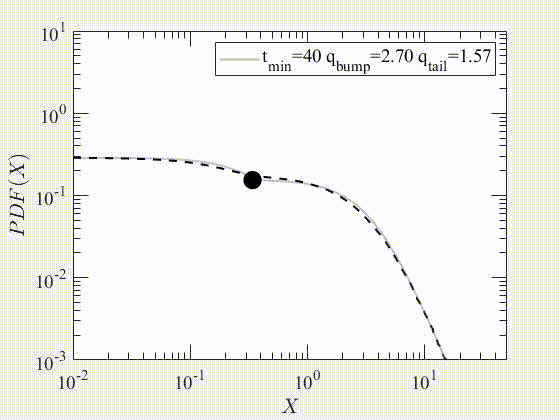
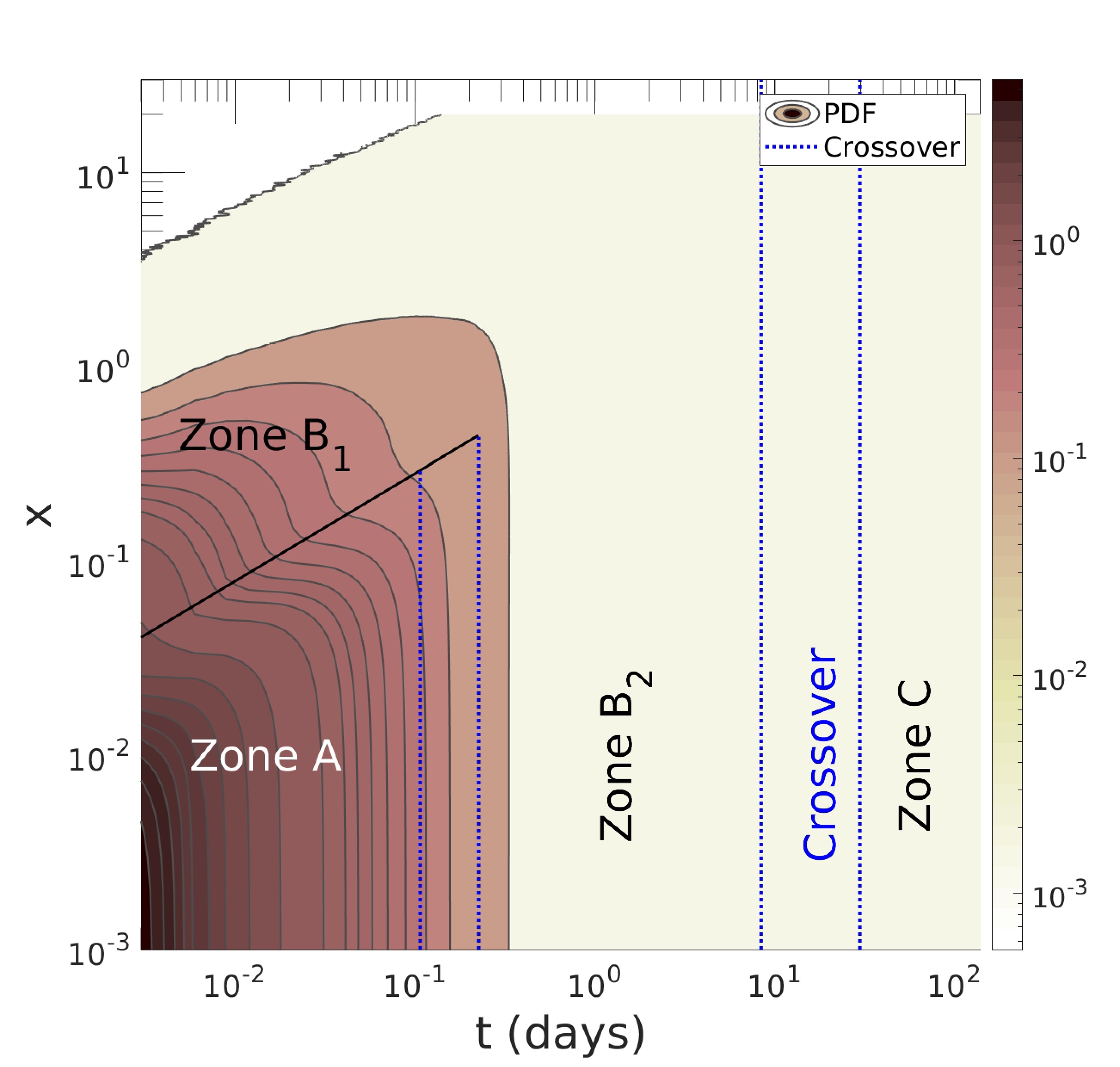
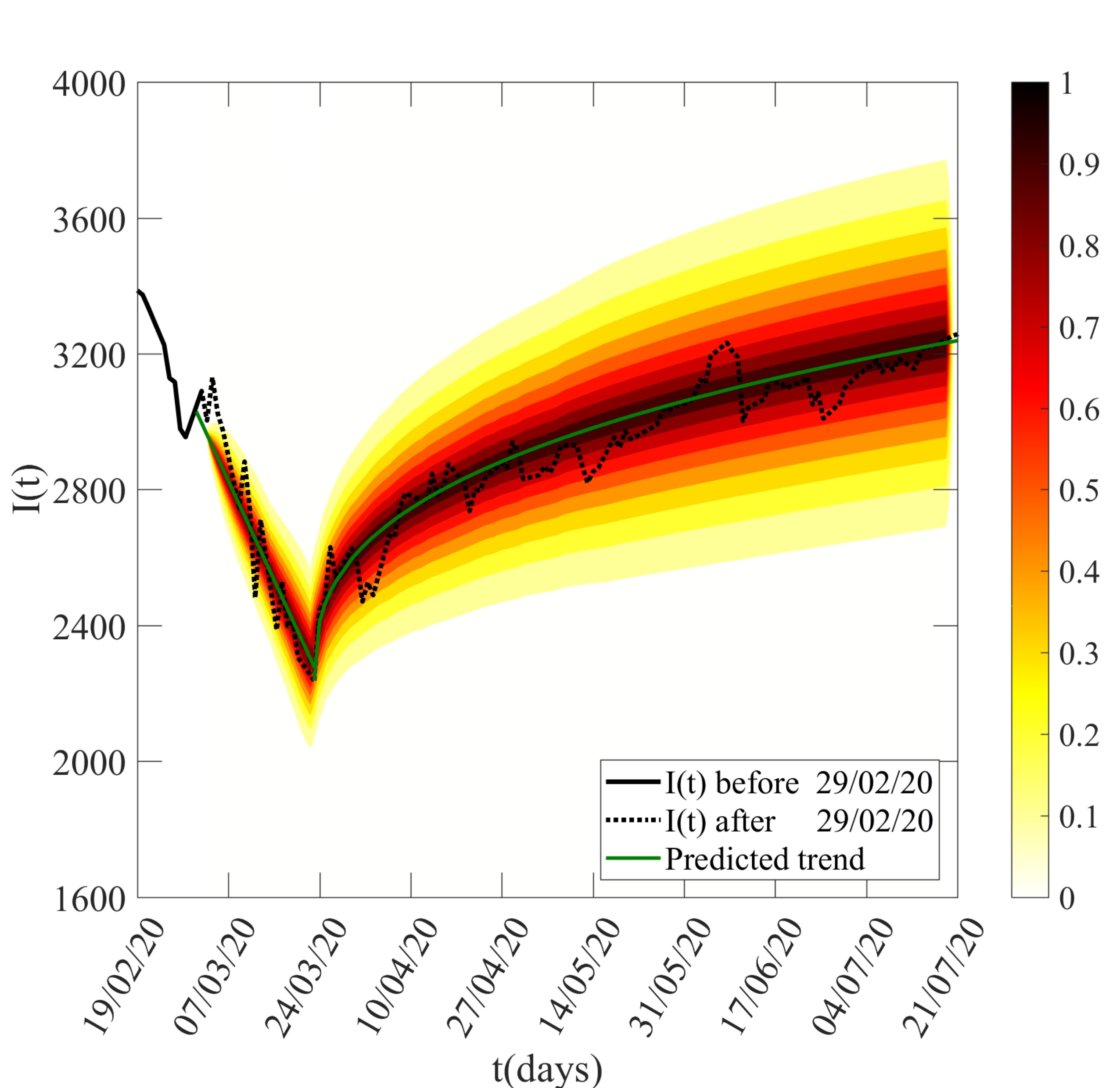
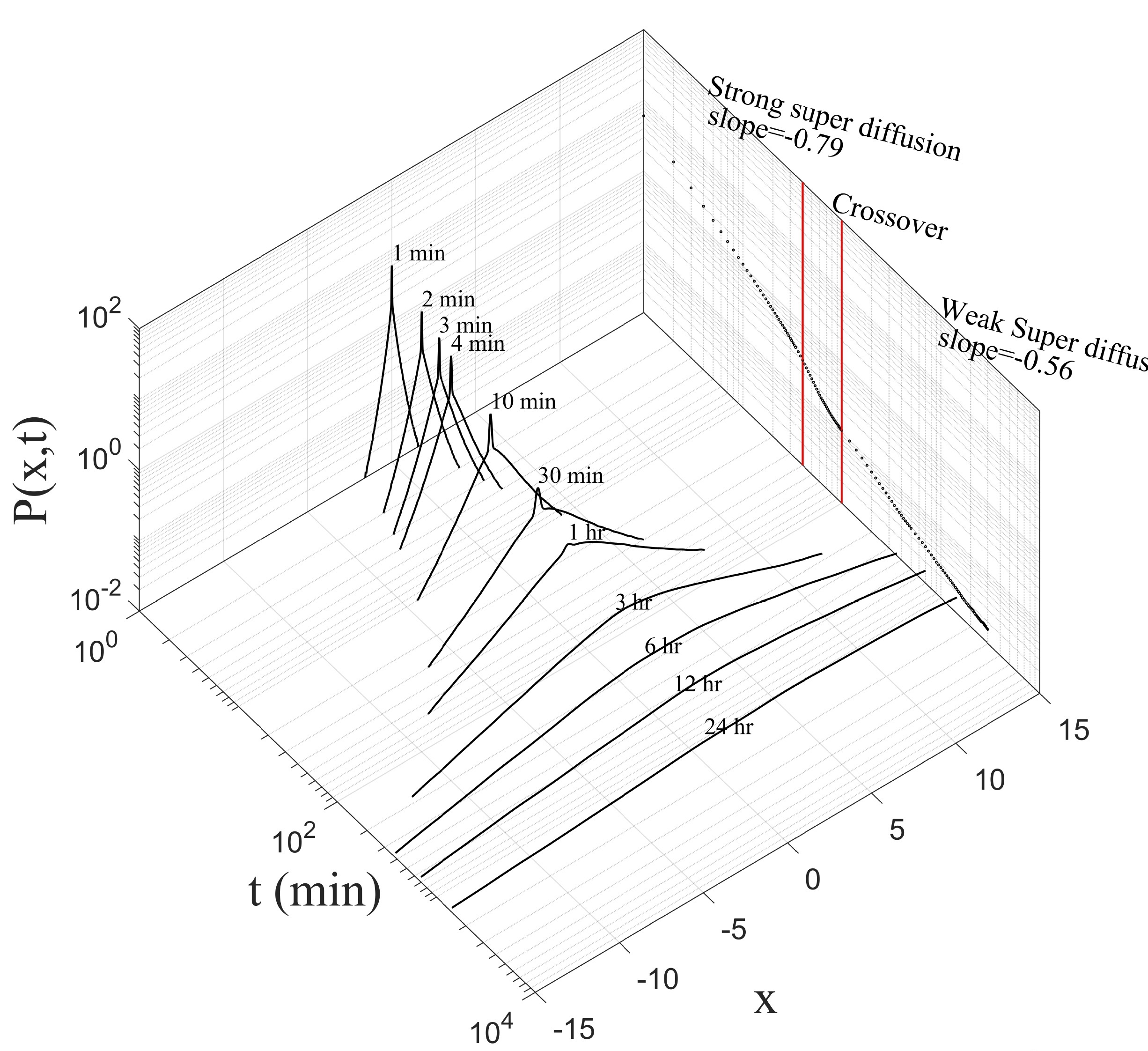
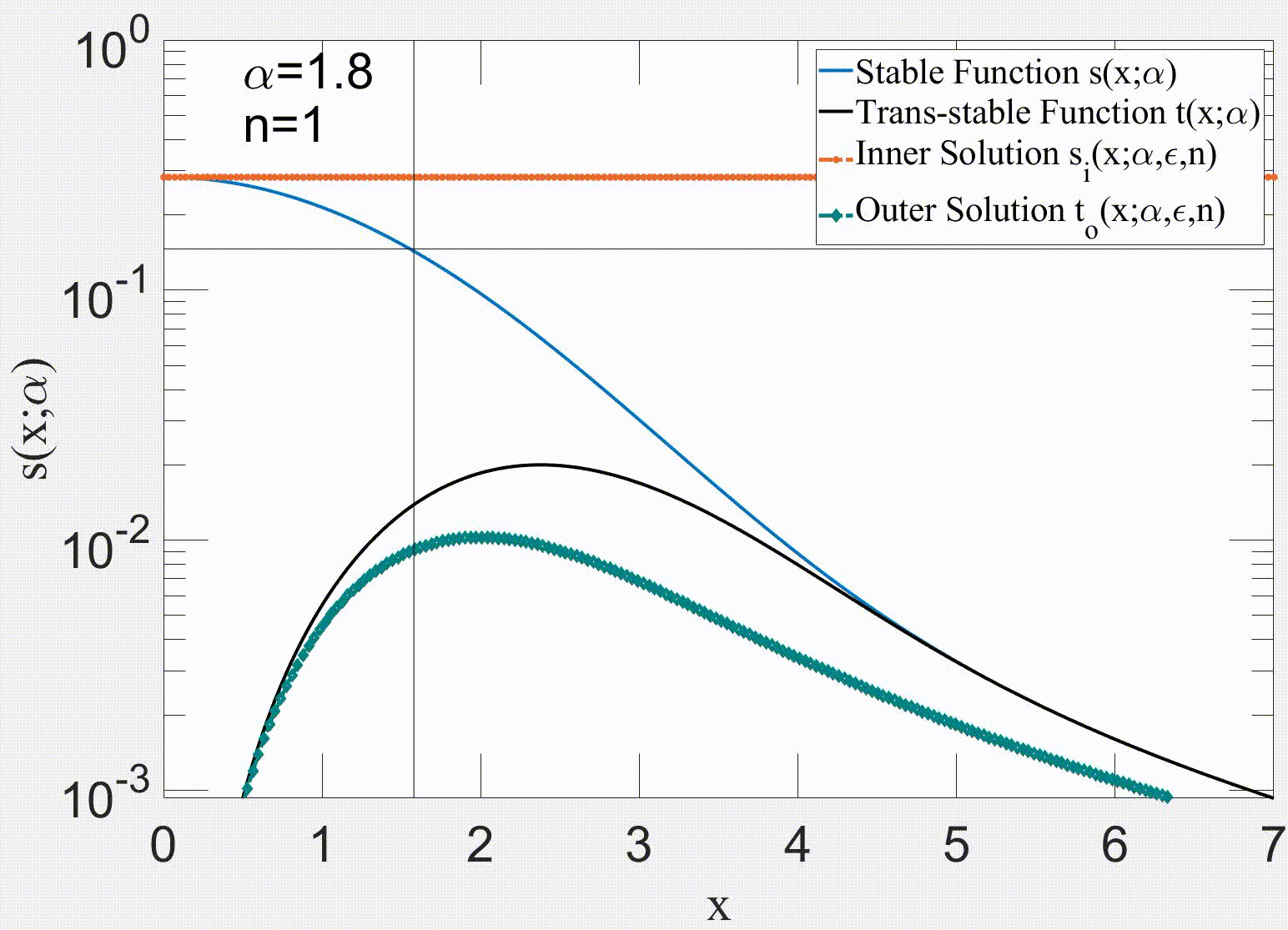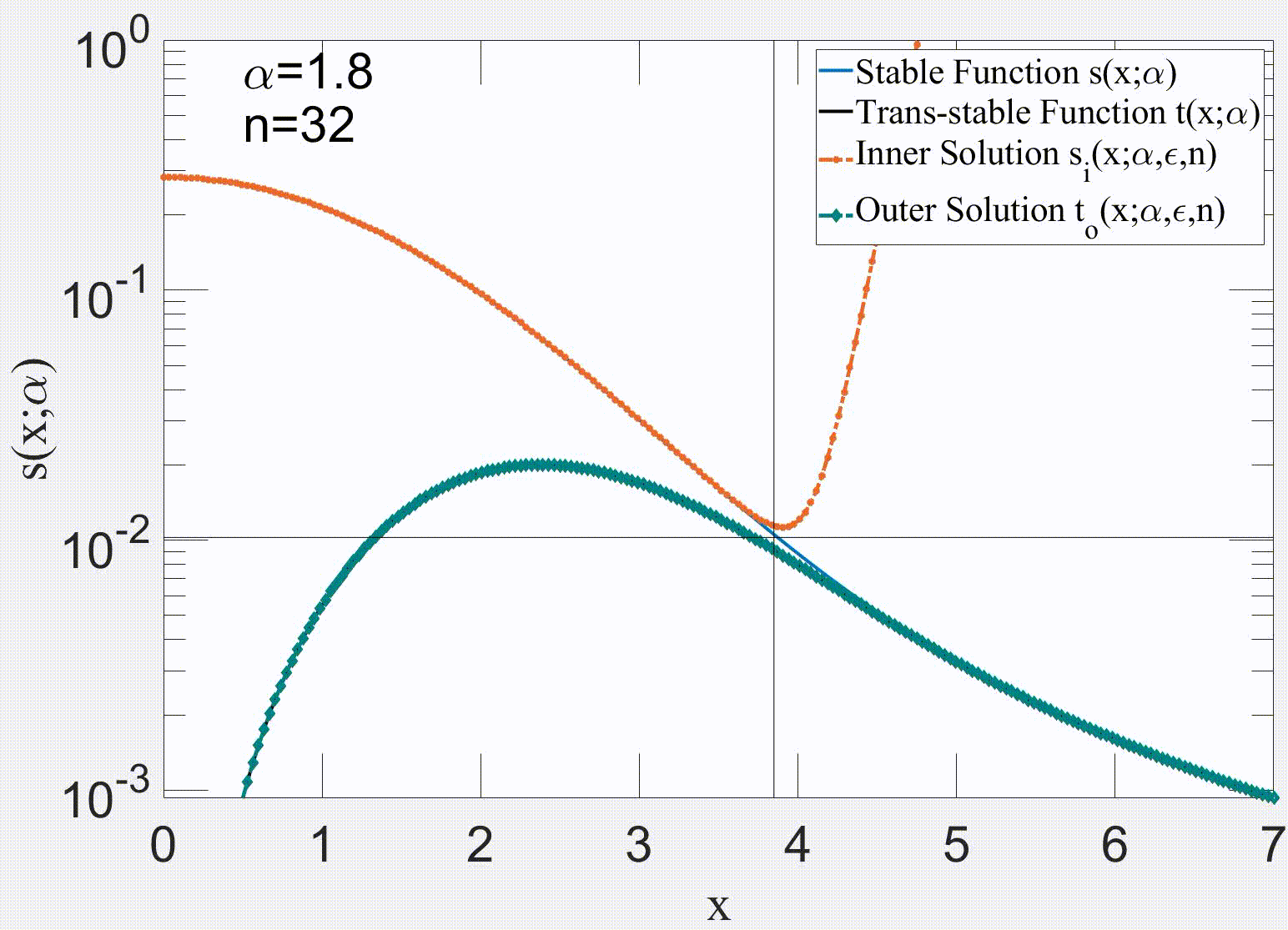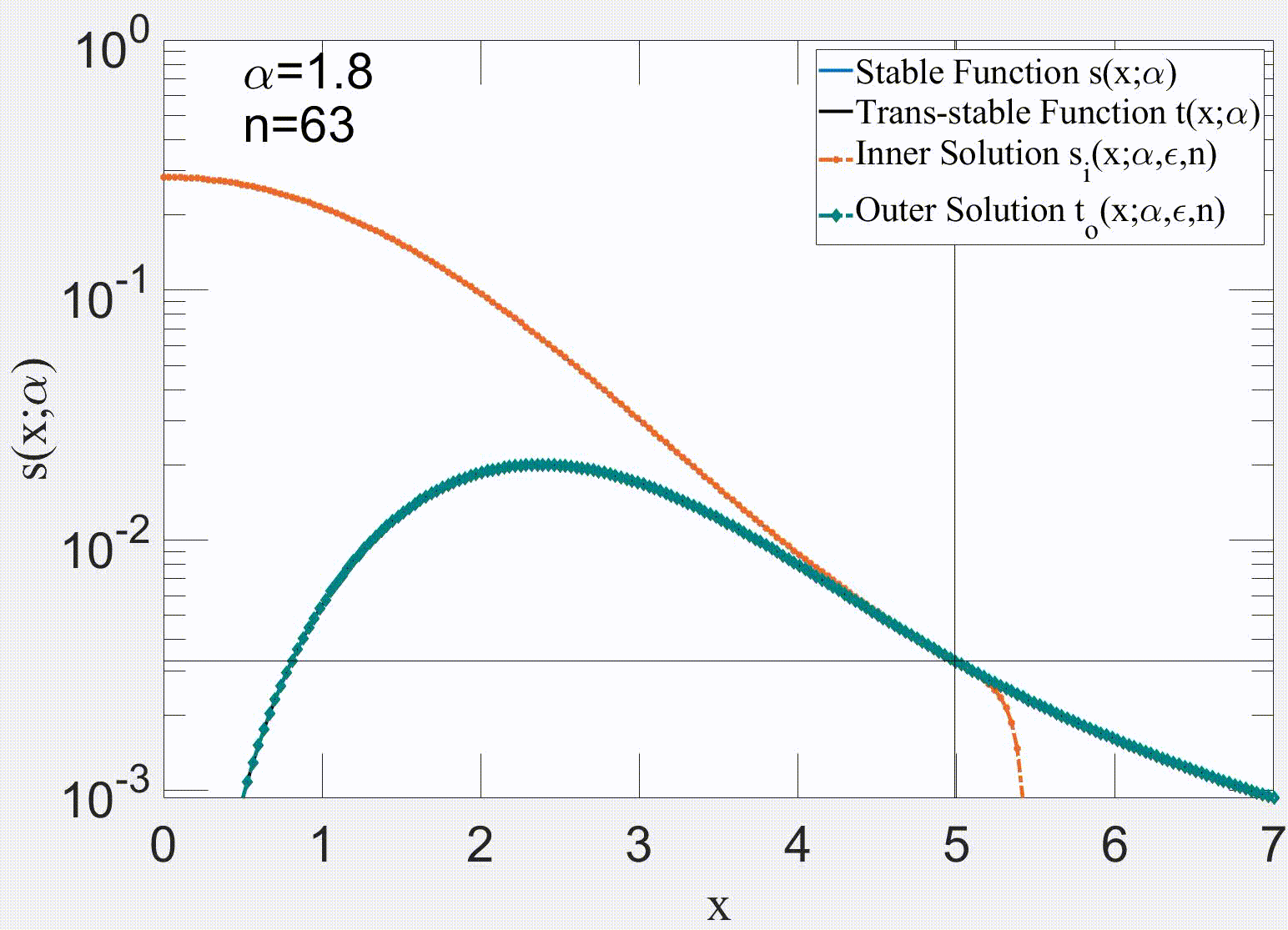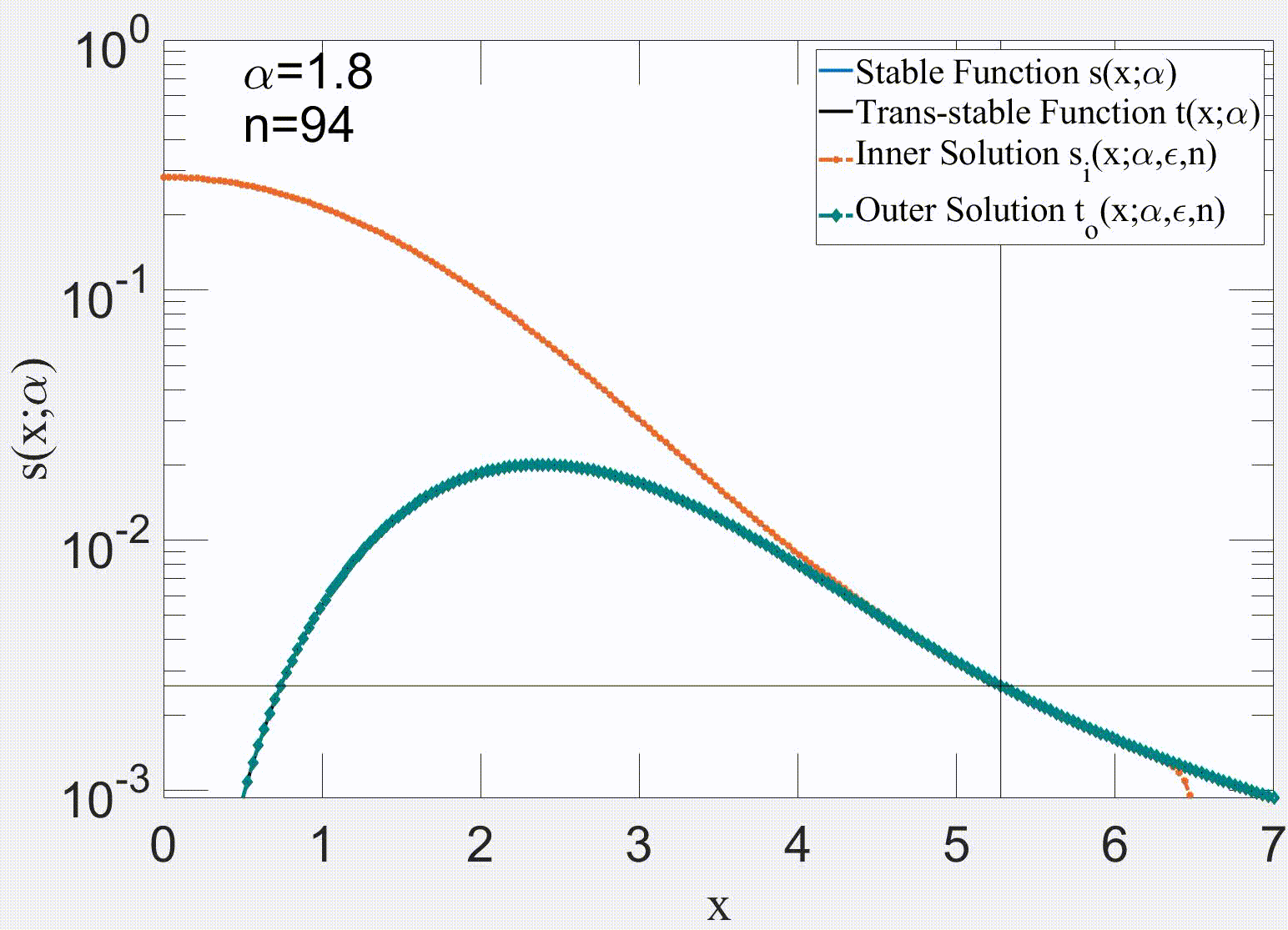
Link: (click here)Our paper makes substantial advances in the analysis of the governing equation of the price return, which yields a new stochastic differential equation (SDE) that tries to cover limitations of Black-Scholes equation (BSE) and its modified versions. Our approach is to decompose the price return into a deterministic component, and stationary q-Gaussian noise. The deterministic term is associated with the systematic risk response to external events that can produce a change in the trend direction. Consequently, our proposed trend is smoother because it depends on the past values of the index. The detrended part is stationary and can be modelled by a q-Gaussian noise. Additionally, this manuscript presents various alternatives for evaluating the stationarity of the detrended price return. Some applied methods include examining the Hurst exponent and the power spectrum of the time series. In general, this paper proposes a methodology to decompose the price return, which can be applied to any index with available historical records for data analysis.